
The 8-Queens problem is one of those classic puzzles that sounds simple but hides a surprising amount of depth. The challenge is this: place eight chess queens on a standard 8x8 board so that no two queens can attack each other. That means no two queens can be on the same row, column, or diagonal.
It’s an elegant test of foresight, logic, and systematic thinking.
A Timeless Challenge of Logic and Strategy
At its core, the 8-Queens problem is a pure logic puzzle masquerading as a chess scenario. You don't need to be a chess master to get it; the rules are straightforward, yet finding a solution is anything but. Think of it less like a game against an opponent and more like solving a tough Sudoku.
Each queen you place on the board adds a new set of constraints, shrinking the number of safe squares for the next one.
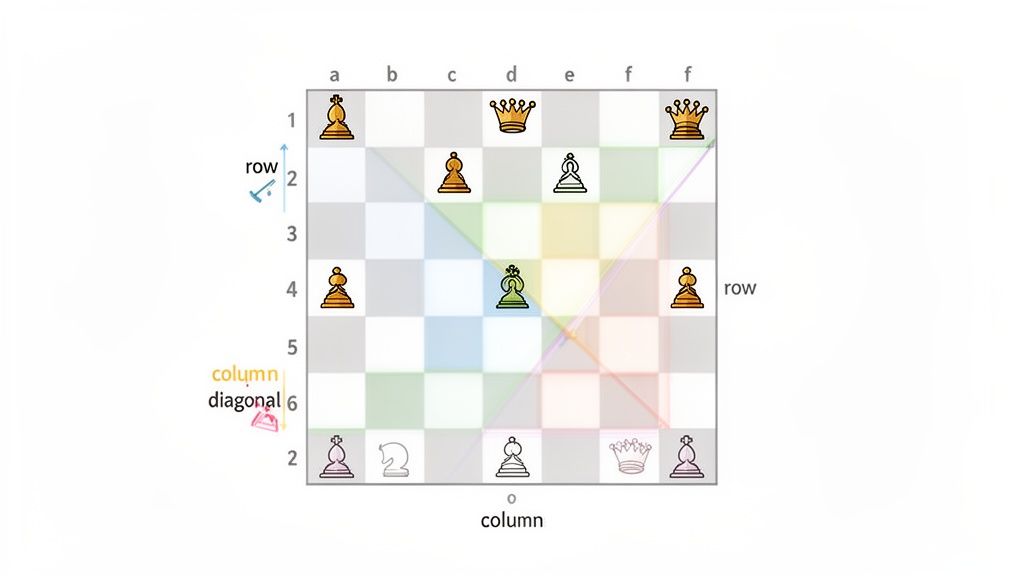
This puzzle is a perfect illustration of constraint satisfaction, where a valid solution has to obey several conditions at once. Here’s a quick rundown of what that means for our queens.
The 8 Queens Problem at a Glance
This table breaks down the puzzle into its essential parts.
| Element | Rule | Goal | | :--- | :--- | :--- | | Board | An 8x8 grid with 64 squares. | Fill the board according to the rules. | | Pieces | 8 queens. | Place all 8 queens successfully. | | Constraints | No two queens can share a row, column, or diagonal. | Satisfy all constraints simultaneously. |
Following these rules is the only way to arrive at a correct solution.
Finding even one valid arrangement is a real achievement, but the challenge doesn't stop there. Mathematicians have figured out there are exactly 92 distinct solutions to the 8-Queens problem. This specific number is what elevates it from a simple brain teaser to a proper mathematical and computational puzzle.
Why Does This Puzzle Matter?
The 8-Queens problem is more than just a historical curiosity. It’s a foundational exercise in computer science and logical reasoning. It’s one of the best ways to introduce important algorithmic concepts, especially backtracking—a method for exploring all possible solutions by systematically trying and discarding paths.
Imagine you're in a maze. When you hit a dead end, you retrace your steps to the last junction and try a different path. That's backtracking in a nutshell.
The puzzle's elegance lies in its simple rules versus its complex solutions. It forces you to think several steps ahead, making it a perfect mental workout for strategic planning and problem-solving.
This guide will walk you through everything, from the puzzle's history to the methods used to solve it, both by hand and with computer algorithms. We’ll explore why this 19th-century brain teaser remains so relevant today, providing a perfect gateway to understanding computational thinking and sharpening your own logical skills.
The History and Mathematical Significance of the Puzzle
 The 8-Queens problem feels like a modern brain teaser, but its story begins long before computers were ever imagined. It first showed up in 1848 in a German chess magazine, Schachzeitung, posed by a chess composer named Max Bezzel.
The 8-Queens problem feels like a modern brain teaser, but its story begins long before computers were ever imagined. It first showed up in 1848 in a German chess magazine, Schachzeitung, posed by a chess composer named Max Bezzel.
At first, it was just a clever riddle for chess lovers to mull over. But its simple rules hid a surprisingly deep complexity, and it wasn't long before it caught the eye of Europe's top mathematical minds. The puzzle was about to transform from a simple game into a gateway for new mathematical ideas.
This growing fascination ensured the problem wouldn't stay a niche hobby. It was on its way to becoming a serious object of study, laying the groundwork for concepts still in use today.
From Chess Riddle to Mathematical Classic
The puzzle’s jump from a magazine curiosity to a maths classic happened fast. In 1850, a mathematician named Franz Nauck republished the problem, and that’s when things really took off. He was the first to correctly state that there are exactly 92 distinct solutions.
That number sparked a much wider investigation. Even the legendary mathematician Carl Friedrich Gauss got interested, thinking about how it would work on a bigger n x n board (the N-Queens problem). His involvement was a clear sign that this was no simple trifle—it was a problem loaded with mathematical potential.
The immediate challenge was to prove Nauck's claim of 92 solutions. This required a methodical way to count every single valid arrangement without missing any or counting the same one twice.
The 8-Queens problem is a perfect example of a constraint satisfaction problem. Every queen you place on the board restricts the available squares for the next one. This forces you to think systematically about a shrinking set of possibilities, which is why it’s still a fundamental teaching tool in computer science.
As mathematicians worked to verify the 92 solutions, they were unknowingly building the logical foundations for search algorithms. They were basically performing a "backtracking" process by hand—exploring placements and then backing up when they hit a dead end.
A Benchmark for Computational Thinking
When computers arrived on the scene, the 8-Queens problem found a new purpose. It became a classic benchmark problem—a standard test used to teach and evaluate algorithms. Its clear rules and known answer make it perfect for demonstrating concepts like recursion and backtracking.
The puzzle’s difficulty also scales dramatically as the board gets bigger, making the generalised N-Queens problem a serious computational challenge. This is great for showing why algorithmic efficiency matters. An algorithm that solves the 8-Queens puzzle instantly might grind to a halt on a 25-Queens board, showing the need for smarter code.
In the UK, the puzzle's legacy continues in universities. A 2016 undergraduate research project at the University of Warwick confirmed that out of 4,426,165,368 possible ways to place 8 queens, only 92 are solutions—a success rate of just 0.00000208%. You can read the full research from Warwick to see the mathematical breakdown.
Today, the 8-Queens problem is a bridge connecting recreational logic, historical mathematics, and modern computer science. It’s a piece of intellectual history that continues to challenge us to find order in a world of complex constraints.
Solving the 8 Queens Problem Manually
Before letting an algorithm do all the heavy lifting, there’s something special about tackling the 8 queens problem with just a pen and paper. Or better yet, a real chessboard. Solving it by hand builds a deep, intuitive feel for the puzzle’s constraints. You’re forced to visualise the board, see conflicts coming, and sharpen your own problem-solving instincts.
Think of it as learning to navigate with a map and compass before grabbing a GPS. When you grapple with the puzzle directly, you gain a much richer appreciation for the elegant logic involved. It makes the algorithmic solutions we’ll get to later feel less abstract and more grounded.
A Practical Starting Strategy
So, where do you begin? Your first move is critical—it shapes the entire attempt. While you can technically start on any square, some offer a clear strategic advantage by immediately cutting down the number of future conflicts.
A common and effective opener is to place the first queen in a corner, like A1 or H8. Why?
- It controls fewer squares: A queen in the centre attacks the maximum number of squares. One in the corner attacks the fewest.
- It simplifies scanning: With the first queen tucked into a corner, it’s visually easier to track its lines of attack and spot safe squares for the next piece.
This isn’t a magic bullet, but it gives your thinking a solid, organised starting point. From there, it’s a methodical cycle: place a queen, then carefully scan for the next safe spot.
The Trial and Error Process
At its core, solving the 8 queens problem manually is all about trial and error. You'll place a queen, then another, and another, until you inevitably hit a dead end where no safe squares are left. This isn't failure; it's a fundamental part of the process.
Let's walk through the thought process:
- Place Queen 1: Let’s start on A1. That immediately takes row 1, column A, and the long A1-H8 diagonal off the table.
- Place Queen 2: Move to the next column (B) and scan for a safe spot. Maybe you find C2. Placing a queen there eliminates row 2, column C, and its two diagonals.
- Place Queen 3: Now for column D. You need a square that isn't under fire from the queens on A1 or C2. You might find a safe space at E3.
- Identify a Dead End: You keep going like this. But then you get to column F and realise every single square is attacked by a queen you've already placed.
This is the moment of truth. When you hit a dead end, you have to backtrack. You remove the last queen you placed (the one in column E) and try to find a different safe square for it in that same column. If there are no other options in column E, you backtrack even further, removing the queen from column D to rethink that choice.
Backtracking is the mental engine for solving puzzles like this. It’s the disciplined act of saying, "This path didn't work, so I'll go back to my last decision and make a different choice." It’s a powerful technique that applies to countless other logical challenges.
This loop—placing, scanning, and backtracking—is how you solve the puzzle. You're exploring a massive tree of possibilities, pruning branches as you find out they don’t lead to a solution. For a broader look at this kind of thinking, our guide on how to solve logic puzzles offers plenty of useful strategies.
Tips for Effective Manual Solving
Keeping track of every attack line in your head can get messy fast. To stay organised and give yourself a better shot at success, try these techniques:
- Use Visual Aids: If you’re using a physical board, put counters or coins on all the squares attacked by the queen you just placed. This creates a clear visual map of safe versus unsafe zones.
- Work Column by Column: A systematic approach is your best friend. By placing one queen in each column from left to right (A through H), you automatically solve the "no two queens in the same column" rule. This really simplifies things.
- Don't Be Afraid to Start Over: If you find yourself backtracking over and over from the same few moves, sometimes it's best to just clear the board. A fresh start with a different opening move can reveal pathways you completely missed before.
Solving the 8 queens problem by hand is a great test of patience and methodical thinking. It’s a truly satisfying mental workout that connects you to the logical heart of this classic puzzle.
Understanding the Backtracking Algorithm
While trying to solve the 8 Queens problem by hand is a fantastic mental workout, you quickly realise how messy it can get. Human intuition is great for spotting a few moves, but it's not a reliable way to find all 92 solutions. For that, we need a more systematic approach.
Enter the backtracking algorithm—an elegant and powerful method computers use to guarantee a complete solution.
Imagine you're navigating a massive maze. You pick a path and follow it, leaving a trail of breadcrumbs. If you hit a dead end, you don't just give up. You simply retrace your steps to the last intersection and try a different route. That’s backtracking in a nutshell: a methodical process of pushing forward, hitting a wall, and smartly retreating to try again.
On the chessboard, the algorithm behaves in a similar step-by-step fashion. It doesn’t guess or rely on instinct. Instead, it explores every potential queen placement, one column at a time, and abandons a path the moment it becomes invalid. This makes it worlds more efficient than a "brute-force" approach, which would test all four billion-plus possible arrangements.
The Core Logic of Backtracking
The algorithm works on a simple, recursive loop. It tries to place a queen in the first safe square of a column, then immediately jumps to the next column to do the same thing. If it successfully places queens in all eight columns, it logs that as a solution.
But what if it reaches a column where no square is safe? That’s the signal that it made a mistake earlier. It "backtracks" to the previous column, picks up the queen it just placed, and tries the next available safe square in that column. This cycle continues until every valid possibility has been explored.
This flowchart breaks down the core logic—placing a queen, scanning for conflicts, and pivoting when stuck.
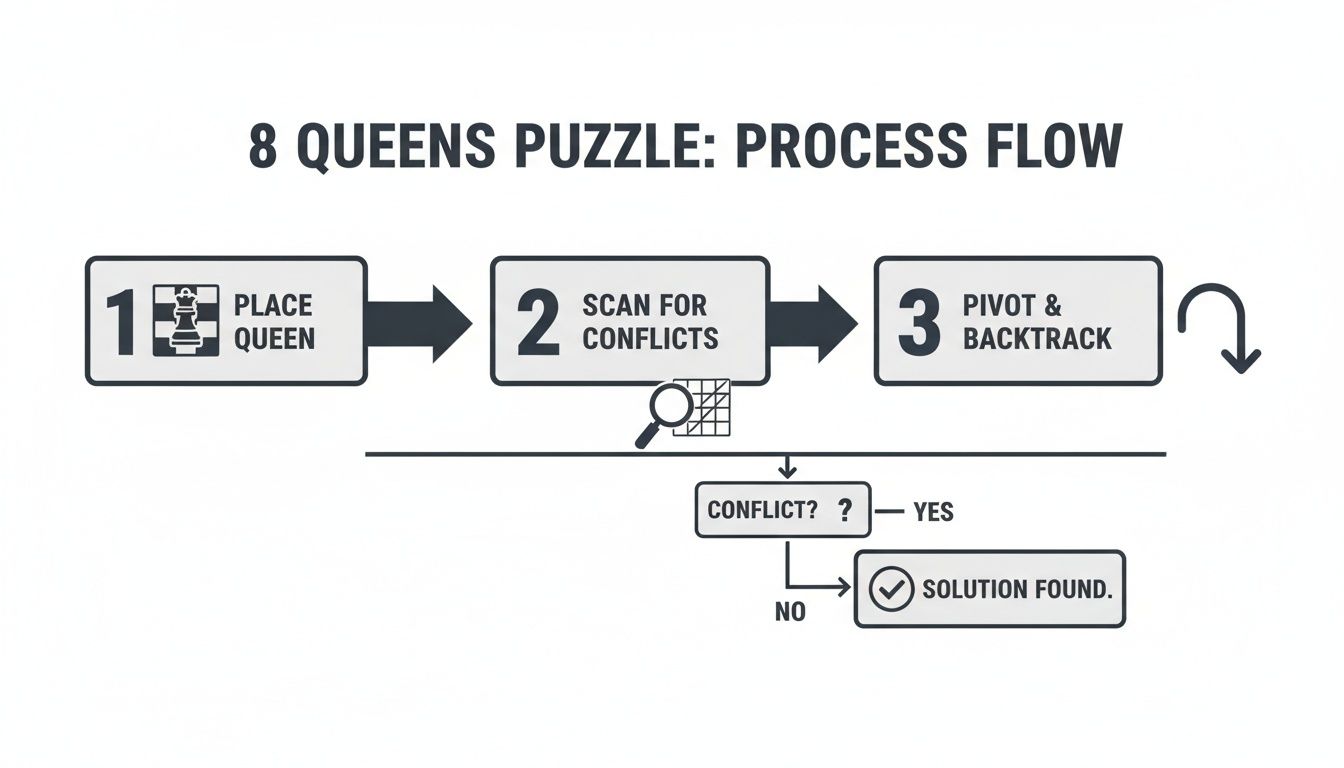
As you can see, it's a clean, repeatable cycle: place, check, and if it fails, backtrack to correct the last decision. This ensures no potential solution is ever missed.
A Step-by-Step Algorithmic Walkthrough
Let's walk through how the algorithm thinks, column by column.
- Start with the First Column: The algorithm begins in column A and places a queen on the first square, A1. So far, so good.
- Move to the Next Column: It moves to column B and scans downwards for the first square not attacked by the queen on A1. It finds B3 is safe and places a queen there.
- Continue Recursively: This process repeats. It moves to column C, finds a safe square, places a queen, then moves to column D. Each placement is like starting a new mini-problem based on the previous step.
- Hit a Dead End: Eventually, the algorithm might get to column F and discover that every single square, from F1 to F8, is under attack from the queens in columns A through E. It's stuck.
- Trigger the Backtrack: This is the magic moment. Since no queen can go in column F, the algorithm knows its last move was wrong. It goes back to column E, removes the queen it placed there, and looks for the next safe square in that column.
- Find a New Path or Backtrack Further: If it finds another safe spot in column E, it places the queen and moves forward to F again with a new board state. If not, it backtracks even further to column D to rethink that placement.
This cycle of placing, advancing, and backtracking continues until all 92 solutions have been methodically uncovered.
Backtracking is essentially a "depth-first search." It dives deep down one path until it either works or fails, only then coming back up to explore other branches. This makes it a perfect tool for solving puzzles with lots of constraints, just like the 8 Queens.
From 8 Queens to N-Queens
One of the best things about the backtracking algorithm is that it scales. The exact same logic for an 8x8 board works on any size N×N board—a challenge known as the N-Queens problem. Whether you're solving for 4 queens or 20, the core process of placing, checking, and backtracking stays the same.
Of course, the problem gets exponentially harder as N grows. While a modern computer can find the 8 Queens solutions in a fraction of a second, finding all solutions for a 25x25 board is a much bigger ask. This scalability is exactly why the N-Queens problem is still a classic benchmark for testing how efficient new algorithms are.
For a deeper dive, check out our guide on the N-Queens problem and its variations.
Ultimately, backtracking provides a beautiful and logical answer to a classic puzzle, turning a chaotic search into a structured and guaranteed process.
Putting Your Skills to the Test
Alright, we’ve covered the history of the 8-Queens problem, walked through how to solve it by hand, and even peeked under the hood at the backtracking algorithm. But theory only takes you so far.
Reading about a strategy is one thing. Applying it when you’re staring at an empty board is another. This is where real understanding happens. Now it’s your turn to step up and see if you can find one of the 92 solutions for yourself.
The best way to make these ideas stick is to get your hands dirty. A good digital puzzle gives you the perfect training ground—no need to set up a physical board, just a clean, interactive space to test your logic. This is how you turn passive knowledge into an active skill.
From Knowledge to Action
Jumping into an interactive puzzle like the Queens Game lets you immediately experiment with the manual strategies we talked about. You can try starting in a corner, working your way across the columns, and feel the trial-and-error process for yourself. It’s this direct interaction that builds mental muscle.
With every queen you place, you’ll start to develop a better gut feeling for spotting conflicts and seeing safe squares. It’s a level of intuition that you just can’t get from reading an article.
- Test Your Strategies: Find out which opening moves click for you.
- Practise Backtracking: Feel what it’s like to hit a dead end and have to methodically retrace your steps.
- Build Spatial Reasoning: Sharpen your ability to see those lines of attack crisscrossing the board.
The point isn't just to find a solution—it's to refine your approach and get better at thinking systematically.
The goal is to bridge the gap between knowing the rules and truly understanding the strategy. An interactive puzzle is the ideal arena for this, offering immediate feedback on every move you make and encouraging you to think more critically about your next placement.
Take on the Challenge
Ready to see how you measure up? The Queens Game gives you a clean, focused environment designed to test your problem-solving skills against this classic puzzle. It strips away all the noise, leaving you with the core challenge: can you place all eight queens so that none can attack another?
There's no substitute for just diving in. Every attempt, successful or not, is a lesson. You’ll see exactly why the 8-Queens problem has captivated people for centuries. And if you enjoy a regular mental workout, you can also explore how daily challenge puzzles keep your problem-solving skills sharp.
The board is yours. Go put your knowledge to the test.
Still Curious About the Puzzle?
Even after digging into the history and solution methods, a few questions usually pop up about the 8 queens problem. Let’s clear up some of the most common ones to round out your understanding.
How Many Solutions Are There to the 8 Queens Problem?
For a standard 8x8 board, there are exactly 92 unique solutions. That’s every possible arrangement where no two queens threaten each other. It’s a fixed, definite number.
But here’s a neat detail: if you account for symmetry—like rotating or mirroring the board—those 92 solutions boil down to just 12 fundamental solutions. Every other solution is just a flipped or turned version of one of those core 12. Knowing there's a concrete number of solutions is what elevates the puzzle from a simple brain-teaser to a classic computational benchmark.
Is the 8 Queens Problem Used in AI?
Absolutely. The 8 queens problem is a textbook example of a constraint satisfaction problem (CSP), a core concept in Artificial Intelligence. A CSP is all about finding a setup that follows a specific set of rules or constraints.
Because its rules are so clear and its difficulty scales up neatly, it’s a perfect tool for teaching foundational AI concepts in university courses. It’s often used to introduce big ideas like:
- State-Space Search: Thinking of every possible board layout as a "state" and then searching for one that solves the puzzle.
- Backtracking Algorithms: As we've covered, this is the smart way to abandon failing paths early—a crucial technique in all sorts of AI applications.
- Heuristic Search: Using "educated guesses" to find solutions faster, which is key to AI optimisation problems.
Think of it as a perfect miniature model for tackling huge, real-world challenges in logistics, scheduling, and planning.
What Is the N-Queens Problem?
The N-Queens problem is what happens when you take the puzzle and scale it up. Instead of a fixed 8x8 board, the challenge is to place N queens on an N×N chessboard so that none can attack each other.
This is where things get computationally interesting. A tiny 4x4 board has just two solutions. An 8x8 board has 92. But by the time you reach a 12x12 board, the number of solutions explodes to over 14,000. For a 27x27 board, the solution count is a massive number with 29 digits.
The N-Queens problem is a fantastic benchmark for algorithmic efficiency. An algorithm that solves 8-Queens instantly might completely choke on a 20x20 board, showing why smart optimisation is so critical.
This exponential growth in complexity keeps the N-Queens problem a relevant and tough challenge for computer scientists today.
Where Can I Play This Puzzle Online?
The best way to really get a feel for the 8 queens problem is to try solving it yourself. Thankfully, you don't need a physical chessboard.
Logic game platforms provide clean, browser-based experiences inspired by this puzzle. They let you test your own strategies without any setup, giving you instant feedback when a placement is wrong. It's an engaging way to backtrack, try a new approach, and sharpen your own logical thinking.
Ready to put your logic to the test? Queens Game offers a polished and engaging browser-based experience that lets you tackle this classic puzzle head-on. Try it now and see if you can find one of the 92 solutions. Play for free at https://queens.game.