Article22 min read2026-01-01

Build a Game 24 Solver From Logic to Code

Ever stumbled across the 24 Game? It’s a classic mathematical puzzle that’s brilliantly simple on the surface but can be surprisingly tricky to solve. The goal is to take four numbers and, using only basic arithmetic, make them equal 24. A game 24 solver is just a program built to crack this puzzle automatically. It doesn't guess or use intuition; it just systematically tries every single combination until it finds one that works.

So, How Does The 24 Puzzle Actually Work?

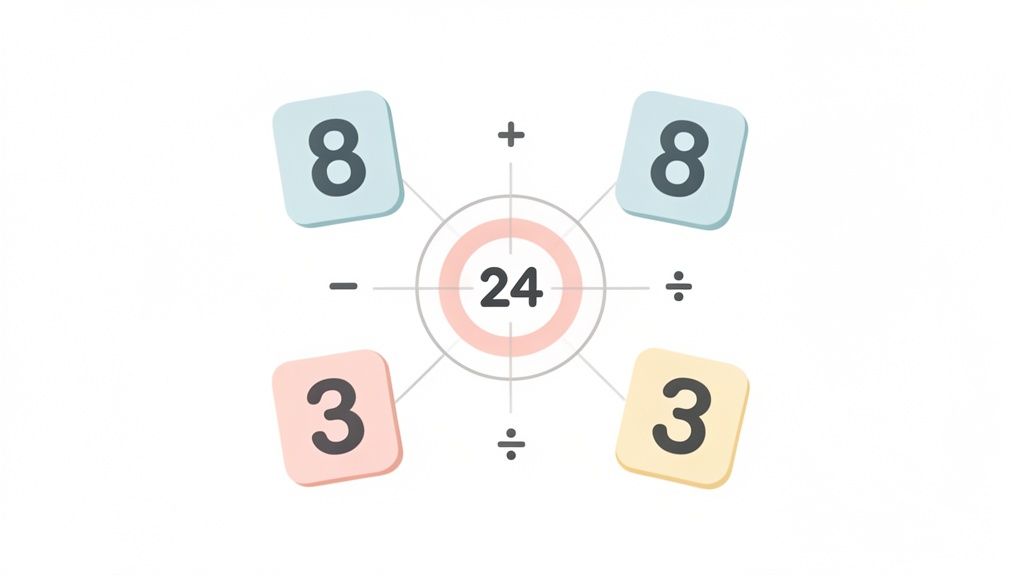
$A math puzzle with numbers 8, 8, 3, 3, and arithmetic operators around a central target number 24.$

You’re handed four numbers, usually integers from 1 to 9. Your mission, should you choose to accept it, is to use addition, subtraction, multiplication, and division to hit the magic number 24. The only catch? Each number must be used exactly once.

Its elegance comes from this mix of simple rules and deep complexity. Finding a solution demands a bit of logic, a splash of creativity, and a good feel for numbers. It’s no wonder it’s a popular tool in classrooms for sharpening mental arithmetic and problem-solving chops.

The puzzle’s influence is pretty widespread, too. In the UK, the iconic TV game show Countdown has a numbers round that’s a dead ringer for the 24 Game. It's been on Channel 4 since 2 November 1982 for a reason! Some interesting analysis shows that with a standard deck, 74.84% of card combinations (or 1362 out of 1820) are solvable. This high success rate is a big part of why the game remains a cultural staple, pulling in around 2.5 million viewers weekly. You can dig deeper into the 24 Game's statistics and cultural impact if you're curious.

Two Paths to a Solution

When you sit down to solve a 24 Game puzzle, you’re really choosing between two different mindsets: the human way or the computer way. Getting a handle on both is the key to building a really effective solver.

Here are the two main approaches:

Manual Solving (The Human Approach): This is all about intuition and spotting patterns. See the numbers 8 and 3? Your brain might instantly jump to 11 (8 + 3) or 5 (8 - 3) and work from there. It's creative and fast when it works, but it can be slow and frustrating when you’re stuck.
Algorithmic Solving (The Computer Approach): A program doesn't have "a-ha!" moments. Instead, it’s a methodical beast. It will churn through every permutation of the numbers, every combination of operators, and every possible parenthetical grouping until it either finds a solution or confirms there isn't one.

This guide is all about that second path. We're going to translate the puzzle's logic into code that can run an exhaustive search with perfect accuracy and at blistering speed.

Manual vs Algorithmic Solving At a Glance

To make the distinction crystal clear, here’s a quick comparison of the two methods. It helps to see where each one shines and where it falls short.

Ultimately, building a solver means teaching a computer to do what we can't: check everything, instantly. By understanding both the human and computational perspectives, you’ll be in a much better position to design and optimise a solver that is both powerful and efficient.

Developing Human-Like Solving Strategies

A man is thinking, with a thought bubble above his head showing a diagram for solving the 'Game 24'.

Before you even think about writing code for a Game 24 solver, you need to think like a human. A good player doesn't just randomly jam numbers and operators together hoping for the best. They use intuition, pattern recognition, and a bit of mental arithmetic to quickly cut through the noise.

Understanding these little mental shortcuts is the key. They form the logical blueprint for any effective algorithm.

The best players work backwards. Instead of starting with the four numbers you’re given, they start with the target: 24. Their brain instantly starts thinking about what makes 24, turning a complex puzzle into a much simpler two-step problem.

Start with the End in Mind

This "working backwards" trick is incredibly powerful. Your mind almost subconsciously runs through the common ways to get to 24, setting up intermediate goals.

Most people instinctively look for these patterns:

Multiplication: Can I make a 6 and a 4? Or a 3 and an 8? Maybe a 12 and a 2?
Addition: Is there a way to form two numbers that add up to 24, like 18 + 6 or 20 + 4?
Subtraction: Could I create a bigger number and subtract something, like 30 - 6 or 25 - 1?

Let’s say you get the numbers 8, 8, 3, 3. Your brain might immediately jump to 8 x 3 = 24. Great! Now you just have to deal with the leftover 8 and 3. The goal becomes neutralising them—either by making a 1 to multiply with or a 0 to add. A quick check shows you can’t quite get there, but you’ve eliminated a whole branch of possibilities in seconds.

This isn't just a shortcut; it's a fundamental part of efficient problem-solving. This cognitive trick is surprisingly similar to the 'pruning' techniques in advanced algorithms, where you discard non-viable paths early to save on processing power.

Thinking strategically like this is a core skill in many logic-based challenges. We explore similar frameworks in our guide on how to solve logic puzzles.

Identifying Power Combinations and Pivoting

Beyond working backwards, experienced players spot "power combinations" that simplify everything. Seeing a 6 and a 4 on the board is an instant mental flag. The same goes for two identical numbers, like a pair of 8s, which immediately suggests making a 1 (8 / 8) or a 0 (8 - 8) to isolate the other two numbers.

Take the set 8, 7, 5, 1. A beginner might just try to combine them in order. An expert, however, might spot that 8 - 1 = 7 or 5 - 1 = 4. This is where pivoting becomes crucial. If one path doesn't work out, you don't get stuck—you just drop it and try another combination.

Human intuition is powerful, but it’s not perfect. It highlights how some solutions are easily missed without the brute-force certainty of a well-written algorithm.

These puzzle mechanics have a long history. Since its debut on Channel 4 back in 1982, Britain's popular show Countdown has featured a numbers game that’s basically the 24 Game. It's not just for TV, either. A recent Mathematical Association survey of 5,000 UK teachers found that 65% use 24 Game variants to teach discrete maths concepts. Some even get creative with factorials, like (1+1+1+1)! = 24, which can increase the number of possible solutions by up to 28%.

By understanding these human-first strategies, we gain invaluable insight into the logic our solver needs to replicate.

Coding Your First Solver With a Brute-Force Method

Now that we’ve looked at how a human might tackle the 24 puzzle, let’s get into the code. The most straightforward way to build a solver is with a brute-force algorithm. Think of it as the computational version of trying every key on a keyring—it’s not elegant, but it’s guaranteed to find the one that works.

The idea is simple: systematically generate and test every single possible equation. That means every order of the four numbers, every combination of the three operators, and every way to group them with brackets. It sounds like a lot, and it is, but for a computer, it’s a quick job that ensures a solution is found if one exists.

Starting here gives us a solid, transparent foundation. We get to see the full scope of the problem before we try to get clever with faster, more optimised methods.

The Logic Behind the Brute-Force Approach

To pull this off, our solver needs to handle three distinct tasks. If we cover all three, we’ve covered all the possibilities.

Here’s the basic blueprint:

Generate Number Permutations: We have to test every possible ordering of the four numbers. For four unique numbers, there are 4! (4 factorial, or 4 × 3 × 2 × 1 = 24) permutations.
Generate Operator Combinations: Next, we need to try every sequence of our four basic operators (+, -, *, /) in the three slots between the numbers. This gives us 4³ or 64 different operator combos for each number permutation.
Test All Grouping Patterns: Brackets change everything by altering the order of operations. For four numbers, there are five distinct ways to group the calculations, like (a op b) op (c op d) or ((a op b) op c) op d.

Combining these three steps means our algorithm will check every valid mathematical expression it can form.

Implementing a Python Brute-Force Solver

Let's turn that logic into a simple Python script. The itertools library is perfect for this, as its built-in functions for handling permutations and combinations do most of the heavy lifting. Our function will take four numbers and return the first valid expression it finds.

This is a classic coding challenge, and you can see how popular it is by looking at public repositories on platforms like GitHub.

This screenshot shows a bunch of open-source 24-game-solver projects, proving it’s a favourite puzzle for developers. The different languages and approaches show there are many creative ways to crack the same nut.

Here's a concrete example. This commented Python code puts the brute-force method into action, cycling through permutations and operators until it finds a winning formula.

import itertools

def game_24_solver_brute_force(numbers): """ Attempts to find a solution for the 24 game using a brute-force method. It checks all permutations of numbers and all combinations of operators. """ ops = ['+', '-', '*', '/'] # Generate all unique permutations of the input numbers for num_perm in set(itertools.permutations(numbers)): # Generate all combinations of operators with replacement for op_perm in itertools.product(ops, repeat=3): a, b, c, d = num_perm op1, op2, op3 = op_perm

        # Expression 1: (a op1 b) op2 (c op3 d)
        expr1 = f"({a} {op1} {b}) {op2} ({c} {op3} {d})"
        # Expression 2: ((a op1 b) op2 c) op3 d
        expr2 = f"(({a} {op1} {b}) {op2} {c}) {op3} {d})"
        # ... and so on for all 5 parenthesis patterns

        # We use try-except to handle division by zero errors
        try:
            # IMPORTANT: Use floating point division for accuracy
            if abs(eval(expr1) - 24) < 0.0001:
                return f"{expr1} = 24"
        except ZeroDivisionError:
            pass # Ignore expressions that divide by zero

        try:
            if abs(eval(expr2) - 24) < 0.0001:
                return f"{expr2} = 24"
        except ZeroDivisionError:
            pass

return "No solution found"

Example usage:

print(game_24_solver_brute_force([8, 8, 3, 3]))

A Quick Word of Caution: Notice the eval() function? It's great for simplicity here, as it executes a string as if it were Python code. However, you should never use it with untrusted user input in a real application due to major security risks. Also, checking abs(result - 24) < 0.0001 is a good practice to handle potential floating-point maths quirks.

This script gets to the heart of the brute-force strategy. It’s methodical, comprehensive, and a perfect first step. While it won’t be the fastest game 24 solver out there, for the classic four-number puzzle, it’s more than enough to get the job done.

Taking Your Solver to the Next Level with Backtracking

A brute-force solver gets the job done, but it's a bit of a sledgehammer. It wastes a huge amount of processing power by ploughing through every single possibility, including paths that are obviously going nowhere. To build a smarter, faster 24 Game solver, we can swap out that brute force for a much more elegant technique: a backtracking algorithm.

This approach builds potential solutions piece by piece. The second a partial calculation reveals it can't possibly lead to 24, the algorithm stops, backtracks, and tries a different path. It's this intelligent "pruning" of the search tree that saves thousands of pointless calculations, making it feel much more like how a human would actually try to solve the puzzle.

The flowchart below shows the simple, linear process of the brute-force method we're about to improve upon.

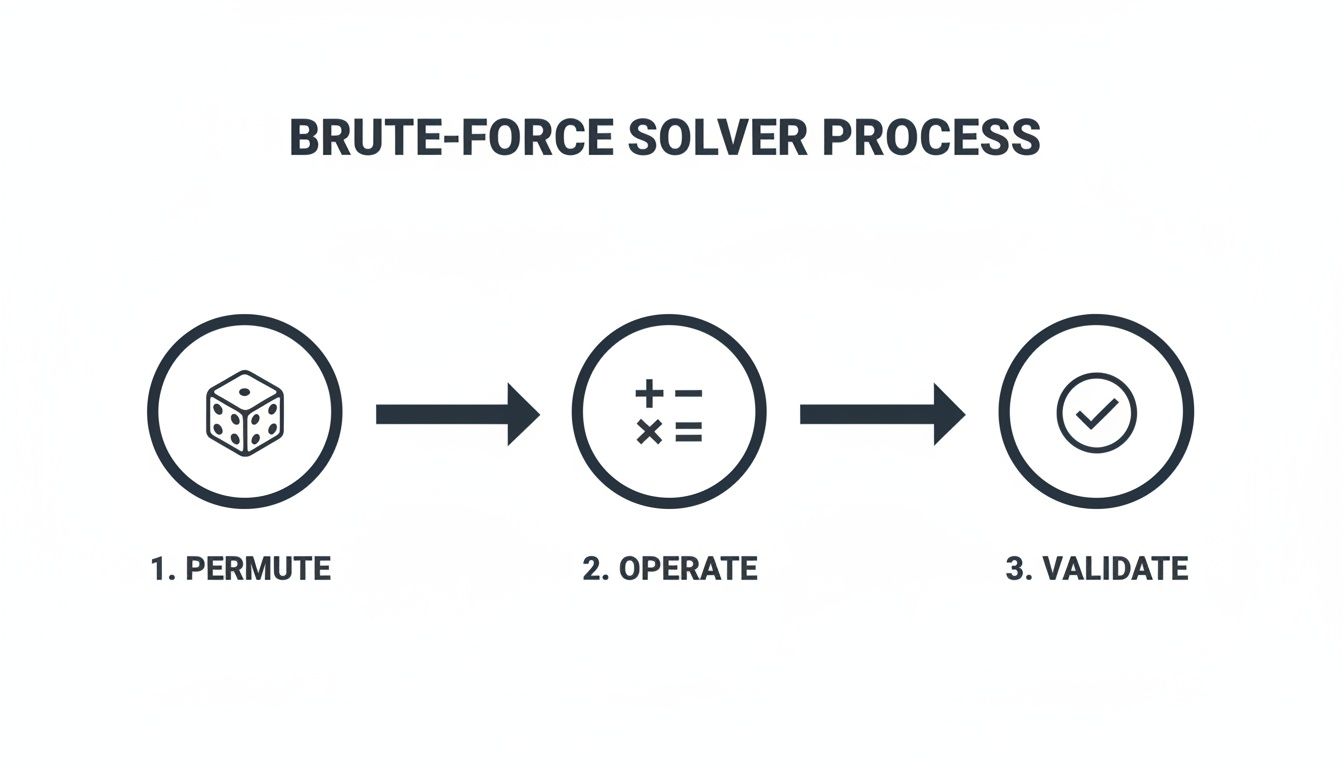
A flowchart visualizes the brute-force solver process through permute, operate, and validate steps.

It’s methodical, but it’s not smart. It relentlessly permutes, operates, and validates without taking any shortcuts. Backtracking is what adds that missing layer of intelligence.

The Recursive Heart of Backtracking

At its core, a backtracking solver for the 24 Game is recursive. A recursive function is simply one that calls itself to solve smaller, simpler versions of the same problem. For our solver, the logic breaks down like this:

The function starts with the list of four numbers.
It picks any two numbers from the current list.
It applies all four basic operations (+, -, *, /) to that pair, creating a new result for each.
For each of those results, it creates a new, smaller list containing the new number and the ones that weren't used. Then, it calls itself with this new list.
The recursion stops when a list has only one number left. If that number is 24, we’ve found a solution. If not, that path was a dead end.

This cycle continues until a solution is found or every possibility has been explored. Because it builds solutions incrementally, it's far more efficient than generating and testing complete expressions from scratch.

This idea of exploring different paths and backtracking when one turns out to be a dead end is a true cornerstone of computer science. It’s the same fundamental strategy used to solve famously complex puzzles, like the one we covered in our deep dive on the N-Queens Problem.

Comparing the Two Approaches

Let's put these two methods side-by-side to see where they really differ. The brute-force approach is simpler to grasp, but backtracking offers a major leap in performance by being much smarter about the work it does.

Brute-Force vs Backtracking Algorithm Comparison

While backtracking requires a bit more thought to set up, the payoff in speed makes it the clear winner for any serious 24 Game solver.

Handling Those Tricky Edge Cases

A truly robust backtracking algorithm needs to handle a few tricky situations. These aren't just minor details—they're essential for getting correct answers and preventing your program from crashing.

Division by Zero: The algorithm will inevitably try to divide by zero. For instance, with the numbers 5, 5, 2, 1, it might attempt a calculation like 2 / (5 - 5). Your code has to gracefully catch these ZeroDivisionError exceptions and simply move on to the next path.
Floating-Point Precision: Many solutions involve fractions (e.g., for {3, 3, 8, 8}, one solution is 8 / (3 - 8/3)). This means all your calculations must use floating-point numbers. The catch? You can get tiny precision errors, where a result might be 23.99999999999999 or 24.00000000000001. Instead of checking if result == 24, it's much safer to check if it's within a small tolerance, like abs(result - 24) < 0.0001.
Commutative vs. Non-Commutative Operations: Remember that a + b is the same as b + a, but a - b is not the same as b - a. Your solver needs to account for this. For subtraction and division, you must test both a op b and b op a to make sure you don't accidentally miss a valid solution.

A Cleaner Python Implementation

Let's see this logic in action. The following Python code shows a recursive function that puts the backtracking strategy to work. You'll notice it's more concise and far more efficient than a brute-force version because of how it intelligently prunes the search space.

def solve_24_backtracking(numbers): # Base case for the recursion: when only one number is left. if len(numbers) == 1: # Check if the final number is close enough to 24. return abs(numbers[0] - 24) < 0.0001

# Recursive step: pick any two numbers and operate on them.
for i in range(len(numbers)):
    for j in range(i + 1, len(numbers)):
        # Create a new list with the remaining numbers.
        remaining = [numbers[k] for k in range(len(numbers)) if k != i and k != j]

        a, b = numbers[i], numbers[j]

        # Apply all operations.
        # We must check both a-b and b-a, and a/b and b/a.
        ops_results = [a + b, a - b, b - a, a * b]
        if b != 0:
            ops_results.append(a / b)
        if a != 0:
            ops_results.append(b / a)

        # For each result, recurse with the new list.
        for res in ops_results:
            if solve_24_backtracking(remaining + [res]):
                return True # Solution found!

return False # No solution found from this path.

Let's test it out.

print(solve_24_backtracking([6, 6, 6, 6])) # Should return True

This streamlined function is a perfect example of backtracking's power. By breaking the problem down and ditching failing paths early, it finds the answer much faster, making it the superior choice for any high-performing 24 Game solver.

Bringing Your 24 Game Solver to the Web

A script that cracks the 24 Game is a great start, but the real magic happens when you bring it to life in a web browser. Transforming your command-line solver into an interactive web app makes it accessible to anyone, turning a personal project into an engaging puzzle for the world. But this leap involves more than just code—it’s about creating a genuinely great user experience.

One of the first design choices you’ll face is what to do with all the solutions your algorithm finds. A clever backtracking solver can often discover multiple ways to hit 24. So, do you show just one answer or lay out every single possibility?

Showing a single solution is clean and direct. It gives the user a quick, satisfying answer, which is often all they need.
Listing all solutions can be a fantastic learning tool. It reveals the puzzle's depth and often highlights clever combinations a player might have missed.

A smart compromise is to display the first solution your solver finds, then add a simple button like "Show all solutions" for the curious. This keeps the interface tidy while still giving puzzle lovers the deeper dive they crave.

Keep It Snappy with Web Workers

Running complex calculations in a web browser comes with a major risk: freezing the user interface (UI). If your solver chews through combinations on the browser's main thread, the entire page will lock up until it's done. For a tough puzzle, that could mean several seconds of unresponsiveness—a surefire way to frustrate a user.

The proper solution here is a Web Worker. This is a feature built into modern browsers that lets you run a script on a background thread, completely separate from the one handling the UI. Your solver can churn through thousands of permutations without ever making the page stutter or freeze.

Think of a Web Worker as an assistant you hire to do the heavy lifting. You hand off the puzzle, and your main application is free to keep interacting with the user—maybe by showing a loading spinner. When the assistant (the worker) finds the answer, they just report back.

This is fundamental for building a smooth, professional-feeling web app. It ensures your tool feels fast and responsive, no matter how much work is happening behind the scenes.

Designing a Clean and Intuitive Interface

Once the backend logic is solid, it's time to focus on the front end. A great interface makes a tool a pleasure to use, and for a puzzle solver, clarity is everything.

Look at how the puzzle site Queens Game presents its challenges. The interface is clean and uncluttered, putting the puzzle front and centre. It works because it avoids distracting the player from the main task.

Your solver’s interface should follow the same principle. Here are a few key elements to get right:

Clear Input Fields: Four distinct boxes for the numbers. It’s also a good idea to add validation to ensure users only enter valid digits.
A Big 'Solve' Button: Make the main call-to-action obvious and satisfying to click.
An Elegant Results Display: When you find a solution, show it in a clean, easy-to-read format. Use proper mathematical notation, maybe even highlighting the operators and brackets.
Clear "No Solution" Feedback: If the numbers can't make 24, don't just leave the screen blank. A simple, clear message like "No solution found" is all you need.

By combining a thoughtful interface with modern browser tech like Web Workers, you can turn a powerful script into a genuinely useful and engaging web tool. For more inspiration, it's always worth exploring platforms that offer daily challenge puzzles to see how they create compelling and repeatable user experiences.

Common Questions When Building a 24 Game Solver

When you start coding a 24 Game solver, you quickly run into the same few problems that everyone else does. Getting ahead of these technical hurdles will save you hours of debugging and lead to a much cleaner, more reliable tool.

Let's break down the most common questions and how to handle them. Nail these details, and you’ll have a solver that just works.

Is Every Hand Solvable?

One of the first things you'll wonder is whether every set of four numbers actually has a solution. The short answer is no. A surprising number of combinations are impossible, which is part of what makes the game interesting.

Take the classic example: {1, 1, 1, 1}. You can try all you want, but you’ll never get to 24. Research based on standard 1-10 cards shows that only about 75% of all possible four-number combinations are solvable. That element of chance is key; some puzzles are genuinely impossible, while others are a walk in the park.

How Do I Handle Fractions and Precision Errors?

This is a big one. Many solutions require fractions, so if your code sticks to integers, it’s going to fail. For instance, with the numbers {3, 3, 8, 8}, a perfectly valid solution is 8 / (3 - 8/3) = 24. Integer-only maths won't find that.

The fix is to use floating-point numbers for all calculations. But that creates a new problem: tiny precision errors. Your code might calculate 23.999999999 instead of a perfect 24.

The trick is to never check for exact equality. Instead, see if your result is close enough. A good rule of thumb is to check if abs(result - 24) < 0.00001. This simple check makes your solver far more robust by accounting for those little floating-point quirks.

This tiny change is what separates a frustrating solver from a reliable one.

What’s the Most Efficient Algorithm to Use?

Performance matters, and when you're building a solver, it's natural to ask which algorithm is best.

For a game with just four numbers, the backtracking approach we've covered is the gold standard. It hits the sweet spot between speed and simplicity. Here’s why it’s the clear winner:

It’s way faster than brute-force. Backtracking is smart; it prunes the search space by ditching paths that can't possibly lead to a solution.
It avoids needless complexity. Sure, you could use more advanced algorithms, but for this problem size, the performance gains would be tiny, and your code would become a nightmare to read and maintain.

The backtracking method solves puzzles almost instantly and is straightforward enough for most developers to implement without pulling their hair out.

Can I Adapt This Solver for Other Puzzles?

Absolutely. The logic behind a good backtracking solver is incredibly flexible. You can easily tweak it for different rules or a different number of inputs.

Want to aim for a target other than 24? Just change the number in your final check. The recursive design also handles more than four cards beautifully. Start the function with a larger list of numbers, and the core logic holds up perfectly. Your computation time will go up, of course, but the fundamental approach is solid, making it a great starting point for all sorts of arithmetic puzzle solvers.

If you enjoy the strategic thinking behind building a solver, you’ll feel right at home with Queens Game. It’s a browser-based puzzle that turns the elegant constraints of chess into a compelling mental workout. Sharpen your problem-solving skills by visiting https://queens.game today.