Article20 min read2025-12-28

Solve the 8 queens puzzle: Backtracking Tips & Visualized Solutions

The 8 Queens Puzzle is a legendary chessboard problem: place eight queens on an 8x8 board so that no two can attack each other. Simple, right? But this elegant challenge has fascinated mathematicians and programmers for centuries.

It’s a puzzle that blends dead-simple rules with a surprising amount of depth.

What Is the 8 Queens Puzzle?

At its core, the 8 Queens Puzzle is a pure test of logic and constraint satisfaction. You have a standard chessboard and eight queen pieces. Your only job is to put them all on the board so that no queen threatens another.

Think of it like setting up eight security cameras in a single room. No camera can be in the line-of-sight of another—not horizontally, vertically, or diagonally.

A chess board displaying various pieces in a puzzle configuration, with ranks and files labeled.

This simple setup forces you to think systematically. With 64 squares and 8 queens, the number of ways you could just drop them onto the board is massive—over four billion. But only a tiny, tiny fraction of those are actual solutions.

The Core Rules Explained

The entire puzzle boils down to three simple, yet powerful, constraints. Getting these into your head is the first step to finding a solution.

To make things even clearer, here’s a quick summary of the rules.

The 8 Queens Puzzle Rules at a Glance

These rules force you to see the board as a single, connected system. Every queen you place has a ripple effect, instantly making a whole set of other squares unavailable.

The challenge isn’t just placing pieces; it’s about seeing the entire web of relationships created by each move. Every queen you place redraws the map of "safe" and "unsafe" squares for the others.

That interplay is what makes solving it so satisfying.

A Brief History of the Puzzle

Though it feels like an ancient brain-teaser, the 8 Queens Puzzle actually has a clear starting point. It was first proposed in a German chess magazine back in 1848 and quickly captured the imagination of mathematicians across Europe.

The problem soon found its way into British mathematical circles, becoming a popular feature in journals and clubs throughout the late 19th century. By the 1870s, it was a staple in British chess clubs, where enthusiasts would share solutions and new variations.

For a deeper dive into its origins, the University of Warwick has an excellent paper on the topic.

Today, it’s still one of the best problems for teaching logic, algorithms, and computational thinking. It's just as relevant now as it was over 150 years ago.

Why This Classic Puzzle Still Matters Today

The 8-queens puzzle might look like a dusty relic from a bygone era, but don't be fooled by its age. Its real power isn't in its history, but in how perfectly it prepares your mind for modern problem-solving. It’s a hands-on laboratory for understanding some of the core ideas in computer science and AI.

At its heart, the puzzle is a classic constraint satisfaction problem. That’s a fancy way of saying you have a goal, but you have to follow a strict set of rules to get there. This isn't just about chessboards; it's the same framework used to tackle countless real-world challenges.

The Detective Analogy: Backtracking in Action

The most popular way to crack the 8-queens puzzle is with an algorithm called backtracking. Think of a detective working a tough case. They follow a promising lead, but if it turns into a dead end, they don't just give up. They carefully retrace their steps to the last choice they made and try a different path.

That's exactly how backtracking works with the queens:

Make a Choice: Place a queen on the first available safe square.
Explore Deeper: Jump to the next row and try to place the next queen.
Hit a Wall: If you get to a row where no square is safe, you’ve hit a dead end.
Backtrack: Go back to the previous row, pick up that queen, and move her to the next safe spot.
Repeat: Keep going until all eight queens are on the board.

This methodical approach—trying something, failing, and smartly retreating—is incredibly powerful. It saves you from checking every single one of the over four billion ways you could place the queens.

Backtracking is the art of failing intelligently. Instead of brute-forcing every combination, it prunes entire branches of possibilities that it knows are dead ends, saving a massive amount of work.

From Chessboards to Real-World Solutions

This "detective" logic is far more than an academic game. The principles behind the 8-queens puzzle are the same ones powering the sophisticated systems we rely on every day. When your GPS app finds the fastest route, it's exploring potential roads and backtracking from traffic jams.

Or think about a university building its course schedule. Every class has constraints—a specific room, a professor, and a time that can't clash with anything else. Organising that chaos is a huge constraint satisfaction problem, often solved using algorithms directly related to the ones used for this puzzle.

Other places you'll find this logic at work:

Logistics and Delivery: Planning the most efficient routes for delivery trucks.
Circuit Design: Arranging tiny components on a computer chip without interference.
Resource Allocation: Assigning staff to projects based on their skills and availability.

When you learn to solve the 8-queens puzzle, you’re not just playing a game. You're building the mental muscles needed to tackle these massive, complex problems. It’s a perfect stepping stone, much like how beginners build their skills with guides that break down different types of chess puzzles for beginners. The 8-queens puzzle is the bridge from simple rules to powerful, real-world thinking.

Exploring Different Solution Methods

With over four billion possible ways to place eight queens on a board, just guessing isn't going to cut it. So, how do you actually solve the 8-queens puzzle? The answer lies in structured, intelligent methods that slice through the noise and find the hidden solutions. These techniques range from the simple (but slow) to the seriously sophisticated, each offering a great lesson in problem-solving.

Let's start with the most basic approach to see why we need something smarter.

The Brute-Force Method: Why It Fails

The brute-force method is exactly what it sounds like: trying every single combination until you stumble upon a solution. You'd generate every possible arrangement of eight queens on the 64 squares and, for each one, check if it works.

While this approach will eventually find all solutions, its inefficiency is staggering. The total number of ways to place 8 queens on an 8x8 board is 64C8, which works out to a colossal 4,426,165,368 combinations. Checking each one would take an insane amount of time, even for a powerful computer. It’s like trying to find a specific grain of sand on a beach by picking them up one by one. It works in theory, but it’s completely impractical.

The failure of brute force teaches us a critical lesson: for complex problems, the path forward isn't more power, but a better strategy.

Backtracking: A Smarter Approach

This is where the backtracking algorithm comes in. It's a far more elegant and efficient technique that mimics a "trial and error with memory" process. Instead of checking every single combination, it builds a solution step-by-step and abandons a path as soon as it breaks a rule.

Think of it as navigating a maze. You follow a path until you hit a dead end. Instead of teleporting back to the start, you just backtrack to the last choice you made and try a different route. This intelligent retreat saves you from exploring countless dead ends.

For the 8-queens puzzle, the process looks something like this:

Place a Queen: Start in the first row and place a queen in the first column.
Move to the Next Row: Go to the second row and find the first column where a new queen isn't under attack.
Check for Dead Ends: Keep doing this, row by row. If you get to a row where no square is safe, you've hit a dead end.
Backtrack and Adjust: When that happens, you go back to the previous row, pick up that queen, and move her to the next safe column.
Resume the Search: From this new position, you start moving forward again, row by row, until you have a full board.

This systematic process prunes massive chunks of the search space, making the problem manageable. You're no longer checking billions of combinations, but instead cleverly navigating a much smaller set of possibilities.

The diagram below shows how the skills learned from puzzles like this connect directly to algorithmic thinking and real-world applications. 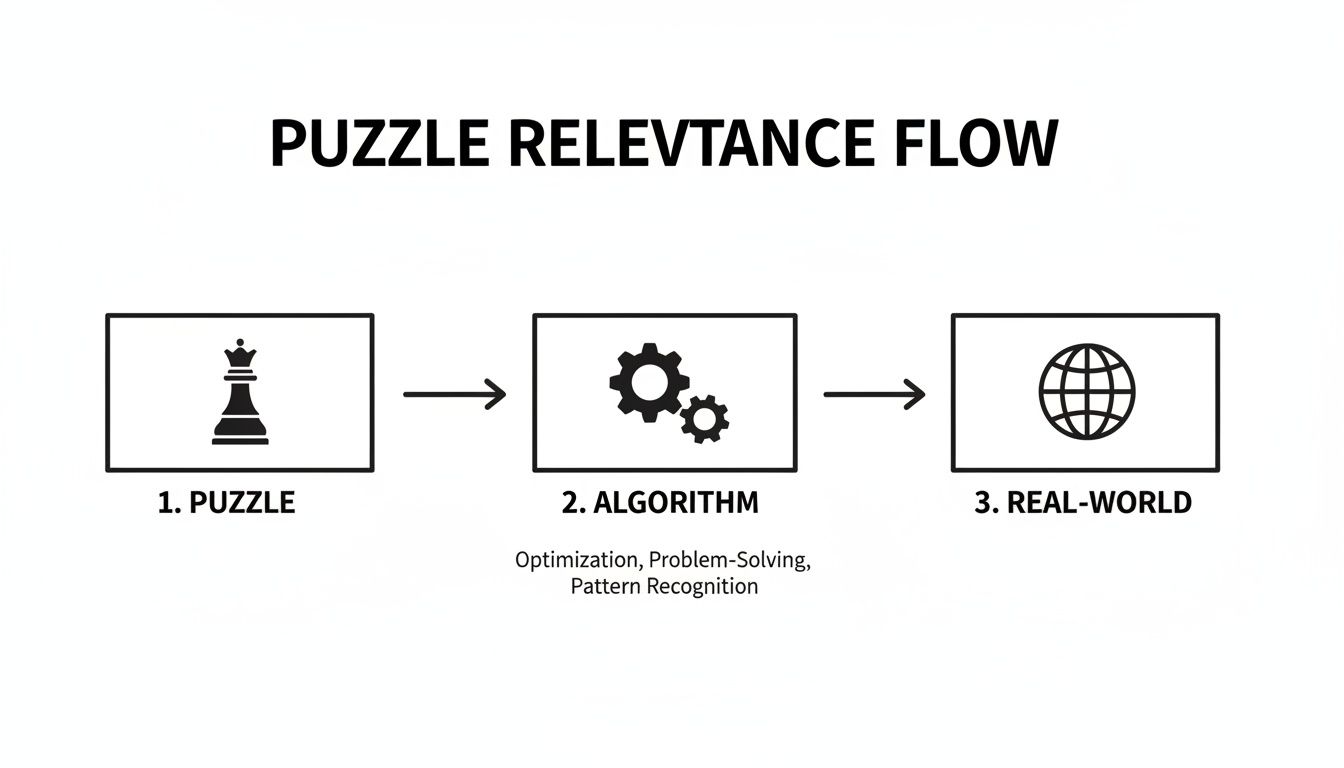Flowchart showing the relevance of puzzles leading to algorithms and their application in the real world. This flow highlights that solving puzzles isn't just for fun; it's a fundamental exercise in developing the logic that powers complex software and systems.

Other Powerful Techniques

While backtracking is the most famous method for solving the 8-queens puzzle, it's not the only one. Other advanced approaches can also crack it, each with its own strengths.

Constraint Programming: This technique defines the problem with variables (queen positions) and constraints (the attack rules). A specialised "solver" then uses logic to find values that satisfy all the rules. It’s like giving a detective the clues and letting them figure it out without any manual guesswork.
Heuristic Algorithms: These methods use "rules of thumb" or educated guesses to find good solutions quickly. They don't always guarantee finding all solutions, but they’re fast. For example, a "greedy" algorithm might always place the next queen in the square that leaves the most safe squares open for future queens.

Each solution method offers a different perspective on problem-solving. Backtracking teaches systematic exploration, constraint programming shows the power of logical deduction, and heuristics show the value of making smart, informed guesses.

Understanding these different strategies gives you a versatile toolkit. If you want to strengthen your systematic thinking, our guide on how to solve logic puzzles offers more insights into building these essential skills. Whether you use a pen and paper or a powerful algorithm, the core principles of structured thinking are exactly the same.

Visualising the 92 Unique Solutions

So, you've seen the methods for finding a solution, but what do they all actually look like? This is where the real beauty of the puzzle starts to click. While an algorithm can churn through possibilities, the patterns only come to life when you see them on the board.

It turns out there are exactly 92 unique solutions to the classic 8x8 puzzle. This isn't a guess; it's a number confirmed through exhaustive computation. Each one is a perfectly stable arrangement where eight queens can stand their ground without threatening each other, satisfying every rule we've covered.

From 92 Solutions Down to 12 Core Patterns

While 92 is the final count, there’s a much more elegant truth hidden inside that number. A huge chunk of these solutions are just rotations or mirror images of each other. Once you account for this symmetry, the 92 arrangements boil down to just 12 fundamental solutions.

Think of it like taking a photograph. You can turn it sideways, upside down, or look at its reflection, but it’s all still the same core image. The 12 fundamental solutions work just like that.

Every single one of the 92 solutions can be generated by taking one of the 12 fundamental patterns and applying a simple transformation: rotating it 90°, 180°, or 270°, or flipping it like a mirror image.

This is a massive insight. It tells us we're not dealing with 92 random layouts, but a structured set of 12 core patterns and their symmetrical twins. Suddenly, the problem feels less about brute force and more about the beautiful geometry at its heart.

A Look at a Classic Solution

To make this less abstract, let’s look at one of the most famous solutions to the 8-queens puzzle. It’s often the go-to example when showing what a finished board looks like.

Here’s a visual of one of the 92 valid arrangements:

Four chessboards displaying chess pieces arranged to illustrate 90-degree rotational symmetry transformations.

In this diagram, you can trace the lines yourself. No two queens share a row, column, or diagonal. It’s a perfect, peaceful configuration.

Using standard chess notation (column, row), the queen positions for this specific solution are:

Take a second to follow the attack lines for a queen or two. You'll quickly see that every path is clear. This one board is the puzzle's rules in action.

Understanding Symmetry in Action

Symmetry is the key that unlocks the other 80 solutions from our 12 fundamental ones. The transformations are simple geometric moves you could do with a real chessboard.

Here are the main transformations involved:

Rotations: Turning the board by 90, 180, or 270 degrees. A valid solution remains valid after any rotation.
Reflections: Flipping the board across its central axis, either horizontally or vertically, to create a mirror image. This new arrangement is also a valid solution.

Interestingly, not all 12 fundamental solutions create the same number of variations. Some solutions have their own built-in symmetry. For instance, if a solution looks identical after a 180-degree rotation, it will only generate four unique arrangements through these transformations, not the full eight. This is why the total isn't a neat 12 × 8 = 96.

By understanding these transformations, you start to see the 8-queens puzzle differently. It’s not a hunt for 92 different answers, but a quest to find 12 unique patterns. This shift in thinking makes the problem feel more solvable and reveals the deep, structural elegance that has captivated thinkers for centuries.

Bringing the Puzzle to Life with Code

Talking about the 8-queens puzzle is one thing, but making it solve itself with code? That’s where you truly get it. The backtracking method feels logical enough on paper, but seeing a computer execute that “try-and-retreat” logic line by line really makes the concept click.

We’ll use Python for this. Its clean, readable style is perfect for showing how an algorithm thinks without getting lost in complex syntax.

A laptop screen displays code related to a queens puzzle, with an arrow pointing to a chess board.

The goal here isn't just to find a solution. It's to write a script that mirrors our own step-by-step thinking. We’ll break the code into small, focused functions, each with a single job. This makes everything much easier to follow, test, and understand.

The Building Blocks of Our Python Solver

To crack the puzzle, our program really only needs to do three things. We can wrap these tasks neatly into their own functions:

Check for Safety (is_safe): This is our "look before you leap" function. Before placing a queen, it checks if the square is safe from any queens already on the board.
Solve Recursively (solve_queens): This is the engine of the whole operation. It tries placing queens column by column, calling itself to go deeper. If it hits a dead end, it backtracks.
Display the Board (print_board): Once a solution is found, we need a simple way to print it out and see the final queen arrangement.

This structure turns a daunting problem into a series of small, manageable steps. Each function is like a specialist tool, and together they explore the board systematically.

A Look at the Python Code

Here’s a hands-on implementation of the backtracking algorithm. I’ve added comments that connect each part of the code directly to the ideas we’ve discussed: placing, checking, and retreating.

A utility function to print the solution

def print_board(board): for row in board: print(" ".join(str(col) for col in row))

A function to check if a queen can be placed on board[row][col]

def is_safe(board, row, col): # Check this row on the left side for i in range(col): if board[row][i] == 1: return False # Check upper diagonal on left side for i, j in zip(range(row, -1, -1), range(col, -1, -1)): if board[i][j] == 1: return False # Check lower diagonal on left side for i, j in zip(range(row, len(board), 1), range(col, -1, -1)): if board[i][j] == 1: return False return True

The main recursive function to solve the N-Queens problem

def solve_queens(board, col): # Base case: If all queens are placed, then return true if col >= len(board): return True # Consider this column and try placing this queen in all rows for i in range(len(board)): if is_safe(board, i, col): # Place this queen in board[i][col] board[i][col] = 1 # Recur to place the rest of the queens if solve_queens(board, col + 1): return True # If placing queen in board[i][col] doesn't lead to a solution, # then remove the queen (backtrack) board[i][col] = 0 # If the queen cannot be placed in any row in this column, return false return False

Example usage for the 8 queens puzzle:

N = 8 board = [[0 for _ in range(N)] for _ in range(N)]

if solve_queens(board, 0) == False: print("Solution does not exist") else: print_board(board)

This script is more than just a block of code; it's the backtracking logic brought to life. The solve_queens function dives down a path, and if it fails, it just returns False. This tells the previous step to undo its move and try something else. It's elegantly simple.

This code gives you a solid foundation for tackling not just the 8-queens puzzle, but a whole family of problems based on constraints. Once you understand this one script, you’re ready for much tougher algorithmic challenges.

The principles here scale up dramatically. In fact, UK academic teams sometimes use massive versions of this puzzle to test new algorithms. While the 8-queens puzzle has 92 solutions, the numbers explode as the board grows. A 10x10 board has 724 solutions, and bigger boards have trillions.

If you’re keen to see how this all works on a larger scale, our article on the generalised N-Queens problem dives much deeper into how these solutions scale.

Your 8 Queens Questions, Answered

Once you get your head around the rules of the 8 queens puzzle, a few questions almost always come up. It's a genuinely curious problem, and digging into these common queries is the best way to really understand what makes it so special.

Let's clear up the most frequent points of confusion, from how many solutions exist to whether there's some secret formula to solve it.

How Many Solutions Does the 8 Queens Puzzle Have?

This is usually the first thing everyone asks. The straightforward answer is there are 92 distinct solutions to placing eight queens on an 8x8 board so that none can attack another.

But there's a more interesting layer to that number. While there are 92 total arrangements, many are just rotations or reflections of each other. If you filter out these duplicates, you're left with just 12 fundamental solutions.

This is a crucial distinction. Those 12 fundamental solutions are the true, unique patterns. Every single one of the 92 board setups can be created by taking one of these core 12 and just flipping or rotating it.

So, while a program hunting for solutions would spit out 92 boards, someone studying the puzzle's deep structure is really just looking for those 12 core patterns. It changes the goal from a brute-force search into a more elegant hunt for unique structures.

Is There a Shortcut or Formula for a Solution?

It's tempting to think there might be a simple mathematical formula—a quick calculation that just gives you the right coordinates. Unfortunately, for the 8 queens puzzle and its bigger relatives, no simple, direct formula exists.

The problem is so tricky because every choice you make is connected. Placing one queen instantly restricts the available squares for all the others. This tangled web of constraints means you can't just calculate positions in isolation.

This is exactly why we need algorithms. Methods like backtracking are perfect for this because they navigate the complex tree of decisions one step at a time. They explore a path, realise it's a dead end, and intelligently backtrack to try something else. The solution isn't found in one neat equation, but through a structured process of trial and error.

Can You Solve the Puzzle on Any Size Board?

Absolutely, and this is where a fun puzzle becomes a classic computer science problem. The 8x8 board is just one example of the much broader N-Queens Problem.

The N-Queens Problem asks: can you place N non-attacking queens on an N×N board? This opens up an infinite family of puzzles, each with its own quirks. You could try solving for 4 queens on a 4x4 board or 100 queens on a 100x100 board.

Here’s a quick look at how the challenge shifts with the board size:

1x1 Board: Trivial. One queen, one solution.
2x2 and 3x3 Boards: Impossible. There are no solutions because the boards are just too small and cramped.
4x4 Board: Has 2 unique solutions.
5x5 Board: Has 10 unique solutions.

Interestingly, solutions exist for all N-Queens problems as long as N is 4 or greater. The number of solutions grows astonishingly fast, which is why it's a great way to test how efficient a search algorithm is. A 10x10 board has 724 solutions, a 12x12 has 14,200, and a 27x27 board has over 234 trillion! This explosive growth really shows why you need a clever algorithm, not just brute force.

Ready to test your own logic and problem-solving skills? The Queens Game offers an interactive, browser-based experience where you can tackle these fascinating placement puzzles firsthand. Move beyond theory and start building your strategic thinking one move at a time. Try it now!