Ever heard of the Eight Queens Problem? It’s a classic puzzle with a beautifully simple premise: place eight chess queens on an 8x8 chessboard so that none of them can attack each other. That means no two queens can be on the same row, column, or diagonal.

Sounds easy, right? It’s anything but.

What Is the Eight Queens Problem?

At its core, the Eight Queens Problem is a pure test of logic and spatial reasoning. Don’t worry, you don’t need to be a chess grandmaster to solve it. You only need to know how the queen moves.

In chess, the queen is an absolute powerhouse. She can move any number of squares horizontally, vertically, or diagonally. This is what makes the puzzle so tricky—every single queen you place on the board dramatically shrinks the number of safe squares for the next one.

The Rules of Engagement for the Eight Queens

The rules are incredibly simple, but they create a fascinating web of constraints. Each queen you place has a ripple effect across the entire board, influencing every move that follows. To find a solution, you have to follow three non-negotiable conditions.

Here’s a breakdown of the core constraints that define the entire challenge:

| Constraint | Rule Explained | Why It Matters | | :--- | :--- | :--- | | No Shared Row | Only one queen is allowed in each of the eight horizontal rows. | This gives you a starting point. You know for a fact that every row must have exactly one queen. | | No Shared Column | Only one queen can occupy each of the eight vertical columns. | Just like the row rule, this ensures the queens are spread out across the board’s width. | | No Shared Diagonal | No two queens can sit on the same diagonal line. | This is the real kicker. It forces you to think in multiple directions at once and is the hardest rule to satisfy. |

Each placement must satisfy all three rules simultaneously. A single mistake, and the entire solution falls apart.

From Chessboard to Code

This puzzle isn't new. It was first posed by German chess composer Max Bezzel way back in 1848. Since then, it’s become a cornerstone of computer science education in the UK and beyond, because it’s the perfect way to teach algorithmic thinking.

Here’s why: there are a staggering 4,426,165,368 ways to place eight queens on an 8x8 board. But out of those billions of possibilities, only 92 are actual solutions. That's a success rate of just 0.00000208%. Trying to find a solution by randomly guessing is practically impossible. You need a smarter approach.

This puzzle teaches a crucial lesson in problem-solving: success often comes not from trying every possibility, but from systematically eliminating the impossible ones.

Its elegant structure makes it an ideal case study for teaching concepts like backtracking, recursion, and constraint satisfaction. If you're new to this kind of thinking, trying out some chess puzzles for beginners is a great way to build the foundational skills needed.

The mental discipline you develop—visualising outcomes, spotting conflicts, and testing ideas methodically—is directly applicable to programming and countless other real-world problems.

Mapping the 92 Possible Solutions

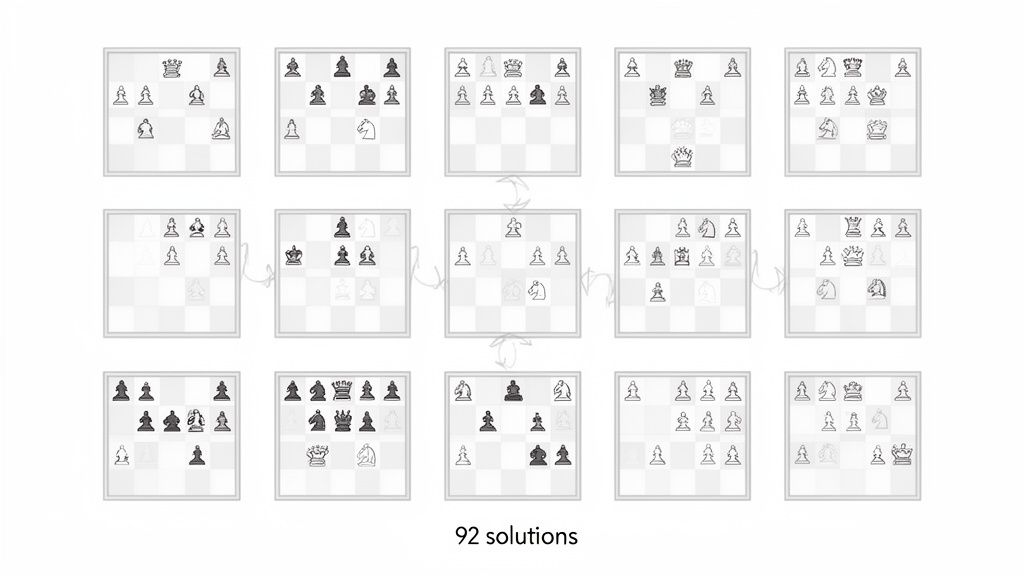
While the rules of the Eight Queens Puzzle sound simple, finding even one solution is tough. Finding all of them is a monumental task. You’re wading through a sea of over four billion possible ways to place the queens, and almost every single one is wrong.

Out of a staggering 4.4 billion potential layouts, it turns out there are exactly 92 distinct solutions. That number wasn’t just a lucky guess; it was confirmed by computers that chewed through every combination. It really puts the difficulty into perspective—the success rate is a tiny 0.000002%.

That incredible scarcity makes each of the 92 solutions a rare and elegant configuration. You can learn more about the math behind this fascinating enumeration problem if you're curious.

Fundamental vs. Total Solutions

You might hear two different numbers thrown around for the solution count: 12 and 92. Both are correct, but they’re counting different things. The bigger number, 92, represents every single unique arrangement on the board.

But if you look closely, many of these 92 solutions are just mirror images or rotations of each other. Think of it like a single photograph that you can flip or turn. It's the same core picture, just viewed from a different angle.

By accounting for these symmetries—like rotations and reflections—we can boil all 92 arrangements down to just 12 fundamental solutions. Every one of the 92 solutions can be generated by transforming one of these 12 core patterns.

Getting this distinction is key. The 12 are the unique building blocks; the 92 are all the ways you can orient those blocks on the board.

Visualising the Core Solutions

Seeing these solutions is the best way to build an intuition for the patterns. Each one is a masterclass in balance, with every queen perfectly placed to avoid conflict.

This diagram shows all 12 of the fundamental solutions.

Notice how the queens are scattered across the board, never lining up vertically, horizontally, or diagonally.

Looking at these patterns reveals some cool properties. For example, some solutions look the same after you rotate them, while others are totally lopsided. This moves the puzzle from being an abstract maths problem to something you can actually see and understand.

These key properties include:

• Rotational Symmetry: Some solutions stay the same if you rotate the board 90 or 180 degrees.
• Reflective Symmetry: Others are perfect mirror images of themselves across a central line.
• Asymmetrical Solutions: Many of the fundamental solutions have no symmetry at all.

By appreciating these 12 core configurations, you start to see the mathematical elegance hidden inside this simple-looking chess puzzle. It stops being about just finding an answer and becomes about understanding the entire landscape of what's possible.

A Practical Step-By-Step Solving Method

Knowing there are 92 solutions is one thing, but finding even one on your own is a whole different challenge. So, how do you actually do it without just guessing? The best way is a smart form of trial and error that programmers call backtracking.

Think of it like solving a maze. You follow a path until you hit a wall. You don't just give up—you retrace your steps to the last junction and try a different route. Backtracking applies that exact same logic to the chessboard.

Why Brute Force Is a Terrible Idea

Before we dive in, let's get one thing straight: just trying every possible combination is a fool's errand. This "brute-force" approach would mean testing every way to place eight queens on 64 squares.

The problem? There are over 4.4 billion combinations. Even if you checked one per second, it would take you more than 140 years to finish. The Eight Queens Problem is a test of logic, not endurance.

Backtracking saves you from this impossible task. Instead of checking billions of options, it helps you eliminate millions of bad placements at once by spotting conflicts early and changing course.

Starting the Search, Step by Step

Let's solve this thing manually. The key is to be methodical. We'll place one queen per column, moving from left to right.

1. Place the First Queen Start with column A. You can place the queen on any of the eight squares, but let’s put it on a1 (the bottom-left corner) for this example. That immediately makes row 1, column A, and the long diagonal from a1 to h8 unsafe.

2. Place the Second Queen Move to column B. We need a safe square.

• Row 1 is attacked by our first queen.
• Row 2 is attacked diagonally by the queen on a1.
• The first safe square we find in column B is b3.

So far, so good. Two queens are on the board, and neither can attack the other. But you can already see how quickly the board is filling up with restricted squares.

3. Place the Third Queen and Hit a Wall On to column C. Let's find a safe spot.

• Row 1 is blocked by the queen on a1.
• Row 2 is blocked diagonally by the queen on b3.
• Row 3 is blocked horizontally by the queen on b3.
• Row 4 is blocked diagonally by the queen on a1.
• The first square that seems safe is c5. Let's place our third queen there.

Now, try to place the fourth queen in column D. Go ahead and check every single square, from d1 to d8. You’ll quickly realise they are all under attack by one of the three queens we’ve already placed. We've hit a dead end.

The Power of Backtracking

This is the moment where backtracking clicks. Our path led to a dead end, so we just need to retrace our steps and change our last decision.

• Step Back: Remove the third queen from c5.
• Try a New Path: Was there another safe square in column C? Yes, c7. Let’s place the queen there instead.
• Continue Forward: Now, with the third queen on c7, try placing the fourth queen in column D again. You’ll find that square d2 is now safe.

This simple process—place, check, and backtrack when you get stuck—is the core of the puzzle. You just repeat this loop until all eight queens are on the board. This systematic approach is a huge part of many logic challenges, a topic we explore more in our guide on how to solve logic puzzles. It builds a mental muscle for problem-solving that goes far beyond any single game.

Understanding the Backtracking Algorithm

So, how do we translate our manual trial-and-error approach into a language a computer can understand? We need a system. The most common and effective way to solve the eight queens problem computationally is an algorithm called backtracking. It’s brilliant because it perfectly mirrors how a human actually solves the puzzle: explore a path, realise it’s a dead end, and retrace your steps to try something new.

Think of it like a detective following a lead. They gather clues and head down a promising path. If that lead goes cold, they don't scrap the entire investigation. They simply go back to the last fork in the road and explore a different clue. That's exactly what backtracking does on the chessboard.

How Backtracking Works in Code

The algorithm starts by systematically placing a queen in the first available column. It then moves to the next column and does the same thing, making sure every new queen is placed in a safe square that isn't under attack by any of the others.

But what happens when it hits a column with no safe squares left? It's a dead end. This is where the magic happens. The algorithm "backtracks"—it removes the queen from the previous column and tries placing it on the next available safe square in that same column. This process continues, pushing forward and backtracking, until a full solution is found.

This core logic—place, check, and backtrack—is the engine that solves the puzzle.

This simple but powerful loop allows the algorithm to navigate the huge number of potential placements without brute-forcing every single one.

A Glimpse into the Code

To give you a feel for how this looks in practice, here’s a simplified Python example. The comments walk you through how each step maps back to our backtracking strategy.

Function to check if a square (row, col) is safe

def is_safe(board, row, col): # Check this row on the left side for i in range(col): if board[row][i] == 1: return False # Check upper diagonal on the left side for i, j in zip(range(row, -1, -1), range(col, -1, -1)): if board[i][j] == 1: return False # Check lower diagonal on the left side for i, j in zip(range(row, len(board), 1), range(col, -1, -1)): if board[i][j] == 1: return False return True

The main backtracking function to solve the puzzle

def solve_queens_util(board, col): # Base case: If all queens are placed, we found a solution if col >= len(board): return True

# Consider this column and try placing a queen in all rows one by one
for i in range(len(board)):
    if is_safe(board, i, col):
        # Place the queen
        board[i][col] = 1

        # Recur to place the rest of the queens
        if solve_queens_util(board, col + 1) == True:
            return True

        # If placing queen in board[i][col] doesn't lead to a solution,
        # then backtrack and remove the queen
        board[i][col] = 0

# If a queen cannot be placed in any row in this column, return false
return False

See? The code is a direct translation of our detective analogy. The solve_queens_util function explores each "lead" by placing a queen. If it doesn't pan out, it backtracks (board[i][col] = 0) to try the next option.

Other Computational Approaches

While backtracking is the classic approach, the eight queens problem is also a fantastic example of a wider category of problems called Constraint Satisfaction Problems (CSPs). This framework is a big deal in computer science, used for everything from scheduling airline flights to designing microchips.

A CSP is all about finding a state that satisfies a given set of rules or constraints. For our puzzle, the variables are the queen positions, and the constraints are the rules of attack.

By looking at the eight queens puzzle as a CSP, we open the door to a whole host of powerful solving techniques from the world of artificial intelligence. These methods give us different ways to reason about the puzzle's tricky constraints.

Comparing Algorithmic Approaches

While backtracking is the go-to, other methods offer different strengths. Here’s a quick overview of how they stack up.

| Algorithm | Core Idea | Best For | | :--- | :--- | :--- | | Backtracking | Explores one path at a time, retreating when it hits a dead end. | Conceptual simplicity and educational purposes. | | Constraint Programming | Defines variables and constraints, then lets a solver find solutions. | Complex, real-world problems with many interdependent rules. | | Genetic Algorithms | "Evolves" a population of random solutions toward a valid one. | Problems where an optimal solution isn't required, just a "good enough" one. |

Each of these methods highlights the puzzle's value as a model for exploring complex problem-solving. For those curious about how these algorithms perform on larger boards, our detailed guide on the generalised N-Queens problem dives much deeper.

Exploring the Broader N-Queens Problem

The eight queens puzzle is a fantastic mental workout, but it’s just one chapter in a much larger story. What happens when you change the size of the board? This question opens the door to the generalised N-Queens problem, where the goal is to place N queens on an N×N board.

This isn't just about making the puzzle bigger; it’s a direct look into the fascinating and slightly terrifying world of combinatorial explosion. As N climbs, the complexity skyrockets. An 8x8 board has 92 solutions, which is manageable. A 20x20 board? That has an incredible 39,029,188,884 solutions.

This exponential jump shows exactly why clever algorithms like backtracking aren't just helpful—they're absolutely essential. Trying to brute-force a larger board would be impossible, even for the most powerful computers. The N-Queens problem is a perfect, real-world example of how a problem's complexity can quickly outrun raw processing power.

How Many Solutions for N-Queens?

The number of solutions for different board sizes grows in a way that’s notoriously difficult to predict. There’s no simple formula to calculate the number of solutions for any given N, which has made it a subject of ongoing mathematical research.

Here’s a quick look at how wildly the solution count balloons:

• 4x4 Board: 2 solutions
• 5x5 Board: 10 solutions
• 10x10 Board: 724 solutions
• 15x15 Board: 2,279,184 solutions
• 27x27 Board: An astronomical 234,907,967,154,122,528 solutions

This explosive growth really highlights the true nature of combinatorial challenges. Each new queen adds another layer of constraints that interact with all the previous ones, making the problem exponentially harder.

The N-Queens problem demonstrates a core principle in computer science: as a problem's scale increases, the importance of a clever, efficient algorithm grows exponentially.

Beyond the Classic Puzzle

The N-Queens framework is so versatile that it allows for countless interesting variations, each challenging your problem-solving skills in new ways. These aren’t just academic exercises; they push you to think more flexibly and deepen your understanding of logical constraints.

Some popular variations include:

• Using Different Chess Pieces: How would you place eight knights or rooks on a board so none can attack each other? Each piece brings a completely different set of rules and constraints to the table.
• Adding Blocked Squares: What if some squares on the board are "forbidden" and can't be used? This variation forces you to adapt your strategy on the fly.
• Torus or "Donut" Boards: Imagine the left and right edges of the board are connected, and so are the top and bottom. This creates new diagonal attack lines that completely change the puzzle's geometry.

These variations transform the classic puzzle into a playground for logical exploration. By seeing the eight queens problem as a starting point, you start to appreciate the rich and complex world of combinatorial puzzles—which is at the heart of what makes games like the Queens Game so endlessly engaging.

Common Questions About the Eight Queens Problem

As you dive into the eight queens puzzle, a few questions always pop up. Here are some quick, straightforward answers to the most common ones.

How Many Solutions Does the Eight Queens Problem Have?

For the standard 8x8 board, there are exactly 92 distinct solutions.

But here’s the interesting part: most of those are just rotations or reflections of each other. If you strip away those duplicates, you’re left with just 12 fundamental solutions. Think of them as the master blueprints.

What’s the Best Way to Solve the N-Queens Problem?

The most effective and widely used method is the backtracking algorithm. A brute-force approach would check billions of combinations, which is wildly impractical. Backtracking is much smarter.

It explores a path, placing queens one by one. The moment it hits a dead end—where no valid move is left—it steps back and tries a different path. This simple "step back" strategy saves an incredible amount of wasted effort.

Backtracking is powerful because it prunes the search tree. Instead of checking every leaf, it cuts off entire branches of impossible solutions early on, making it perfect for complex puzzles like this.

Does the Eight Queens Puzzle Have Any Real-World Use?

Absolutely. While it looks like a simple board puzzle, its underlying structure is a classic example of a constraint satisfaction problem. This category of problem shows up everywhere.

• Logistics and Scheduling: Think of optimising delivery routes or assigning tasks to computer processors.
• Circuit Design: Arranging components on a chip to prevent them from interfering with each other.
• AI and Operations Research: Solving all kinds of resource allocation and optimisation challenges.

The logic you use to solve the eight queens puzzle is the same thinking applied to these massive, real-world scenarios.

Do I Need to Be a Chess Expert to Solve This?

Not at all. This is a puzzle about logic, pattern recognition, and methodical thinking—not chess strategy. The only thing you need to know is how a queen moves: horizontally, vertically, and diagonally.

It’s a fantastic mental workout for anyone looking to sharpen their problem-solving skills, regardless of whether you've ever played a game of chess in your life.

---

Ready to put your logical skills to the test? At Queens Game, we’ve turned this classic puzzle into a clean, interactive experience you can play right in your browser. Sharpen your mind and try to find a solution at https://queens.game.